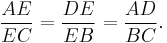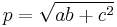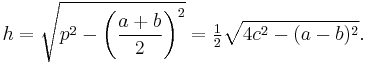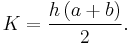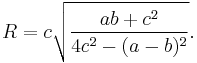Isosceles trapezoid
In Euclidean geometry, an isosceles trapezoid (isosceles trapezium in British English, also known as a symtra[1]) is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides, making it automatically a trapezoid. Some sources would qualify all this with the exception: "excluding rectangles." Two opposite sides (bases) are parallel, the two other sides (legs) are of equal length. The diagonals are of equal length. An isosceles trapezoid's base angles are equal in measure.
Any non-self-crossing quadrilateral with exactly one axis of symmetry must be either an isosceles trapezoid or a kite.[1] However, if crossings are allowed, the set of symmetric quadrilaterals must be expanded to include also the antiparallelograms, crossed quadrilaterals in which opposite sides have equal length. Every antiparallelogram has an isosceles trapezoid as its convex hull, and may be formed from the diagonals and non-parallel sides of an isosceles trapezoid.[2]
Contents |
Special cases
Examples of isosceles trapezoids are rectangles and squares.
Characterizations
If a quadrilateral is known to be a trapezoid, it is not necessary to check that the legs have the same length in order to know that it is an isosceles trapezoid; any of the following properties also distinguishes an isosceles trapezoid from other trapezoids:
- The diagonals have the same length.
- The base angles have the same measure.
- An isosceles triangle is formed by the base and the extensions of the legs. (Rectangles are excluded here.)
- The segment that joins the midpoints of the parallel sides is perpendicular to them.
- Opposite angles are supplementary,which in turn implies that isosceles trapezoids are cyclic quadrilaterals.
- The diagonals divide each other into segments with lengths that are pairwise equal; in terms of the picture below,
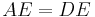 ,
, 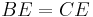 (and
(and 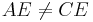 if one wishes to exclude rectangles).
if one wishes to exclude rectangles).
If rectangles are included in the class of trapezoids then one may concisely define an isosceles trapezoid as "a cyclic quadrilateral with equal diagonals"[3] or as "a cyclic quadrilateral with a pair of parallel sides."
Angles
In an isosceles trapezoid the base angles have the same measure pairwise. In the picture on the right, angles 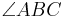 and
and 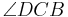 are obtuse angles of the same measure, while angles
are obtuse angles of the same measure, while angles 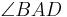 and
and 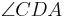 are acute angles, also of the same measure.
are acute angles, also of the same measure.
Since the lines 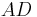 and
and 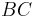 are parallel, angles adjacent to opposite bases are supplementary, that is, angles
are parallel, angles adjacent to opposite bases are supplementary, that is, angles 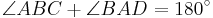 .
.
Diagonals and height
The diagonals of an isosceles trapezoid have the same length and divide each other into segments of the same length. In the picture below, the diagonals 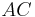 and
and 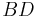 have the same length, that is
have the same length, that is 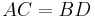 ; and they divide each other in segments of the same length, that is,
; and they divide each other in segments of the same length, that is, 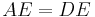 and
and 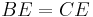 .
.
The ratio in which each diagonal is divided is equal to the ratio of the lengths of the parallel sides that they intersect, that is,
The length of each diagonal is, according to Ptolemy's theorem, given by
where a and b are the lengths of the parallel sides AD and BC, and c is the length of each leg AB and CD.
The height is, according to the Pythagorean theorem, given by
Area
The area of an isosceles (or any) trapezoid is equal to the average of the lengths of the base and top (the parallel sides) times the height. In the diagram to the right, if we write 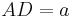 , and
, and 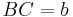 , and the height
, and the height  is the length of a line segment between AD and BC that is perpendicular to them, then the area K is given as follows
is the length of a line segment between AD and BC that is perpendicular to them, then the area K is given as follows
If instead of the height of the trapezoid, the length of the leg 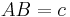 is known, then the area can be computed using the formula
is known, then the area can be computed using the formula
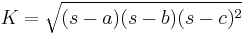 ,
,
where 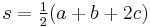 is the semiperimeter of the trapezoid. This formula is analogous to Heron's formula to compute the area of a triangle.The previous formula for area can also be written as
is the semiperimeter of the trapezoid. This formula is analogous to Heron's formula to compute the area of a triangle.The previous formula for area can also be written as
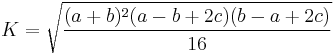 .
.
Circumradius
The radius in the circumcribed circle is given by
In a rectangle where 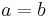 this is simplified to
this is simplified to 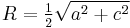 .
.
See also
References
- ^ a b Halsted, George Bruce (1896), "Chapter XIV. Symmetrical Quadrilaterals", Elementary Synthetic Geometry, J. Wiley & sons, pp. 49–53, http://books.google.com/books?id=H3ALAAAAYAAJ&pg=PA49.
- ^ Whitney, William Dwight; Smith, Benjamin Eli (1911), The Century Dictionary and Cyclopedia, The Century co., p. 1547, http://books.google.com/books?id=ownpAAAAMAAJ&pg=PA1547.
- ^ Mzone.mweb.co.za